The Theory
or How to create better images
Why combine?
How many frames?
Calibration: how to use dark, flat and bias frames
Which ISO speed?
The Calibration Process
Below you will find some simple
information, however nothing can replace experience.
Some experts have decided to create an astrophotography dedicated web
magazine which is full of precious, often hard earned knowledge.
Some past topics include Understanding
noise in images, Drizzle discussion, Guiding imaging and much more.

Note: I am in no way related to this magazine or any
advertisement that you may find in it.
I am only putting this banner because an issue is available for free and full
of useful information.
Why combine?
The answer is simple: only to increase the Signal to Noise Ratio (SNR).
Is the resulting image more luminous? No.
Is the resulting image more colorful? No.
The goal of combing many images into one is only to increase the SNR. The
resulting images are neither more luminous or more colorful but they contain
much less noise which will let you stretch the histogram a lot more which will
give you more freedom to bring back colors and details.
|
The example on the
right shows the resulting image from a stack of 1, 2, 4, 16 and 32 images.
No calibration was done and some hot pixels are visible in some cases (no
dark and bias subtraction, no flat division).
Mouse over the text to see the result of the stack for
1 image
2 images
4 images
16 images
32 images
You can see that the resulting image is not
lighter or more colorful when the number of stacked light frames is
increasing but is much smoother.
|

One Light Frame |
How many frames?
The more, the better but above some threshold it is less efficient.
The signal to noise ration in increasing with the square root
of the number of combined frames regardless of the exposure time of each frame.
This is true with all the combining methods (average, median, kappa-sigma
clipping, auto-adaptive weighted average, ...) except entropy weighted average
since this one in using the entropy to weight each pixel and thus is increasing
the noise that is a big entropy contributor..
This means that if your base SNR is 1, when you
combine 10 images the SNR increases by 3.16 (square root of 10). For 30 images
it is 5.47, for 50 images it is 7.07, for 100 images it is 10, for 300 images it
is 17.32.
As you can see to gain a 7 ratio 50 frames are
needed between 1 and 50, but 200 frames are needed above 100.
Are 100 x 1 minute and
10x10 minutes giving the same result?
Yes when considering the SNR but definitely No when considering the final result.
the difference between a 10 minutes exposure and a 1 minute exposure is that the
SNR in the 10 minutes exposure is 3.16 higher than in 1 minute exposure.
Thus you will get the same SNR if you combine 10
light frames of 10 minutes or 100 light frames of 1 minute. However you will
probably not have the same signal (the interesting part). Simply put you will
only get a signal if your exposure is long enough to catch some photons on most
of the light frames so that the signal is not considered as noise.
For example for a very faint nebula you might get
a few photons every 10 minutes. If you are using 10 minutes exposures, you will
have captured photons on each of your light frames and when combined the signal
will be strong.
If you are using 1 minute exposures you will capture photons only for some of
your light frames and when combined the photons will be considered as noise
since they are not in most of the light frames.
Can I combine two (or more) resulting images?
Absolutely, the square root rule applies with a small twist.
When combining two images the SNR increases by 1.414 (square root of 2).
If both images have the same SNR then this is the same as doing a single stack.
That does not mean that the combination is giving the same image, just that the
SNR will be the same.
However if one stack contains more light frames than the other, the SNR of the
two stacks will be different and the SNR of the combination will be lower than
the SNR of a single stack containing all the light frames.
Thus by combining the result of a 10x1 minute stack with a single 1 minute frame
the SNR is roughly the same as the one obtained by combining 2 light frames.
This is due to the fact that when combining two images the noise is additive and
the best image is damaged by the worse image in the process.
Calibration:
how to use dark, flat and bias frames
The calibration is the process consisting
in subtracting the bias and dark signals and dividing by the flat signal.
The goal here is not to explain how to take dark, bias and flat frames (see
here) but to better understand how to
use them to get the best possible images.
A good idea
Everybody is saying that you must take dark, bias and flat frames to create
great images, but if you are doing it the wrong way you can easily damage your
nice light frames ending up with very disappointing results.
The good news is that it is really easy to get
nice results. Here is why and how.
A common misconception
It is a common misconception to think that the number of dark, bias and flat
frames is related to the number of light frames.
A lot of people are using very few (sometimes even only one) dark, bias and flat
frames while they could get much better results by using a large number of dark,
bias and flat frames with the same set of light frames.
Following the square root rule you will have much cleaner masters if you use a
lot of frames to create them. Remember that you are trying to remove the dark
and bias signals, not the noise that is coming with it.
For example when you subtract the master dark from each light frame you are
adding the noise of the master dark to the noise of the light frame. The smaller
the noise of the master dark, the less noise you will add to the light frame.
This is also true for the master bias and the master flat.
In fact by using only a very small number of frames for the creation of the
masters you can easily triple the noise of the calibrated light frame (bias and
dark subtracted and flat divided) compared to the noise of the light frame
before calibration.
You will then need 9 times (3 squared) more light
frames to bring back the noise to the level you could have had by using noise
free masters.
This is the reason why you should use as many
dark/bias/flat frames as possible. On the practical side, 20 frames is a minimum
if you want to not add too much noise, and 50 to 100 will give you really nice
and (almost) noise free masters..
A side note about hot pixels
Hot pixels are pixels that are not behaving normally. They are a very strong
signal that is visible in each dark and each light frame.
Of course when you subtract one dark frame to one light frame you will remove
the hot pixels which may give the false impression that the dark subtraction did
its job.
However, at the same time the subtraction doubled the noise of the calibrated
light frame and ruined it thoroughly.
Which ISO speed?
The question is common enough and the
answer is simple: it doesn't matter...sort of.
In fact the ISO speed is just a setting of any DSLR, but since the CMOS or CCD
chip is the same (you don't change it when changing the ISO speed, do you?) then
the results are really the same.
This is not because you are using a higher ISO speed that you get more photons,
it's just that the signal is more amplified (noise and all).
The good news is that you don't
need to change the ISO speed to try to capture a fainter target. You just need
to take longer exposures.
Of course it's a little more complicated than that since there is a good ISO
speed for each DSLR.
However it depends on the characteristics of each sensor chip (readout noise and
electronic noise) and is not simple to compute.
Christian Buil has computed the values for a few Canon DSLRs
| DSLR |
Recommanded (Optimal) ISO
Speed |
| Canon EOS 10D
|
400
(290) |
| Canon EOS 20D |
1000 (1000) |
| Canon EOS 350D |
800
(900) |
| Canon EOS 5D |
1000 (1100) |
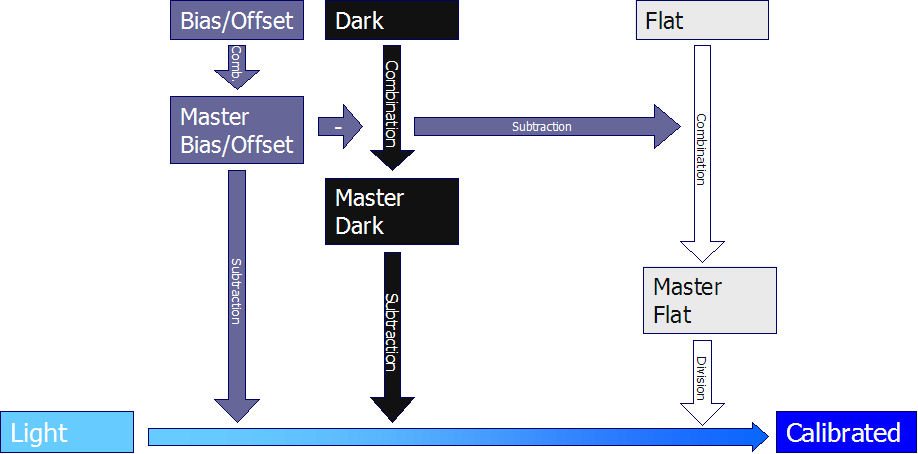
The Calibration Process
The calibration process and how each set
of files (lights, darks, flats,...) is used is often perceived as a
mystery but is in fact quite simple.
Below is the full calibration process when all the files are available:
Full Calibration Process (all
files available)

However it is common and perfectly possible to properly calibrate without using
dark flat frames. The calibration process in this case is described below:
Alternate Calibration Process
I (no dark flat frames)
On the other hand if you are
using dark flat frames you can also perfectly calibrate without using bias
frames. Here's the process in that case:
Alternate Calibration Process
II (no bias frames)

Any other combination leads to
improper calibration so you should stick with one of these 3 possibilities.





